XChiChiX


這不是很戲劇化的發展嗎

c031: 00264 - Count on Cantor

  • 1377 字
  • 次閱讀
  • 則評論
  1. 1. 內容
  2. 2. 範例輸入
  3. 3. 範例輸出
  4. 4. 想法
  5. 5. 程式碼

CPE 一顆星

題目連結:https://zerojudge.tw/ShowProblem?problemid=c031

內容

現代數學中有一個有名的證明（由Georg Cantor所提出的）：有理數是可數的。他使用一個圖表（Cantor’s 列舉）列舉出有理數，如下圖所示：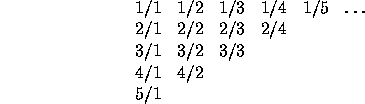

在此圖中，第一項是1/1,第二項是1/2,第三項是2/1,第四項是3/1,第五項是2/2,以下依此類推。

每筆資料一列，有一個整數 n (1 <= n <= 10^7)，輸出在Cantor’s 列舉圖中的第n項。

範例輸入

3
14
7

範例輸出

TERM 3 IS 2/1
TERM 14 IS 2/4
TERM 7 IS 1/4

想法

1 2 6 7 15
3 5 8 14
4 9 13
10 12
11

可以從 1, 3, 6, 10, 15, 21 …，這個數列來看，找出第一個大於 n 的數，看此數在數列中是奇數項還是偶數項，就可以進行運算，求出在圖表中的值。

假設 n = 14
發現數列中第一個大於 n 的數為 15 為第五項(奇數)，設為 sum
已知 15 在圖表中的值為 1/5
設 c = 5(第五項)
1+sum-n / c-sum+n = 1+15-14 / 5-15+14 = 2/4
得到 n 在圖表中的值為 2/4 #

若是偶數項，則公式為
c-sum+n / 1+sum-n

程式碼

C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <bits/stdc++.h>
#define fastio ios_base::sync_with_stdio(false), cin.tie(nullptr)
using namespace std;

int main(){
    fastio;
    int n, sum, c;
    while(cin >> n){
        sum = c = 0;
        while(sum < n){
            ++c;
            sum += c;
        }
        if(c & 1){
            cout << "TERM " << n << " IS " << 1+sum-n << "/" << c-sum+n << "\n";
        }
        else {
            cout << "TERM " << n << " IS " << c-sum+n << "/" << 1+sum-n << "\n";
        }
    }
    return 0;
}